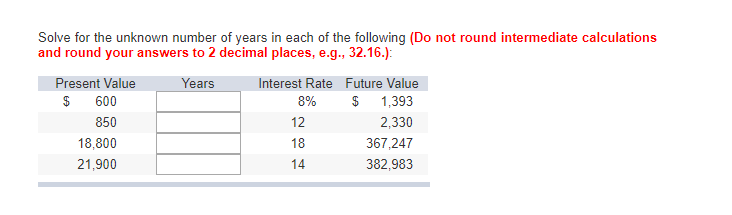

Solve for the unknown number of years in each of the following (Do not round intermediate calculations and round your answers to 2 decimal places, e.g., 32.16.) Present Value Years $ 600 850 8,800 21,900 Interest Rate Future Value 8% $ 1,393 2,330 367,247 382,983 12 18 14












